Semillero de Investigación GIA - Simulador Calculo Diferencial
SimuladorCalculo Diferencial

Limites
Límite de una función
El límite de una función f(x) cuando x se aproxima a un valor c, denotado como:
lim (x→c) f(x), es el valor L al que se acercan los valores de f(x) a medida que x se acerca a c, pero sin necesariamente alcanzarlo.
En otras palabras, el límite describe el comportamiento de una función en las proximidades de un punto, independientemente de si la función está definida o no en ese punto.
Para entender qué son los límites, consideremos un ejemplo. Empezamos con la función f(x) = x + 2

El límite de f en x = 3 es el valor al cual se aproxima f a medida que nos acercamos más y más a x = 3. Gráficamente, es el valor de y al que tendemos en la gráfica de f al acercarnos más y más al punto de la gráfica donde x = 3.
Por ejemplo, si partimos del punto (1,3) y nos movemos en la gráfica hasta estar muy cerca de x=3, entonces nuestro valor y (es decir, el valor de la función) está muy cerca de 5.

Fuente: Geogebra
Similarmente, si empezamos en (5,7) y nos movemos a la izquierda hasta estar muy cerca de x = 3, el valor y nuevamente estará muy cerca de 5.
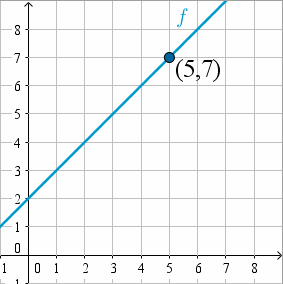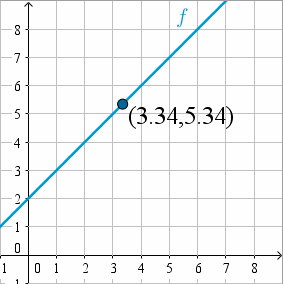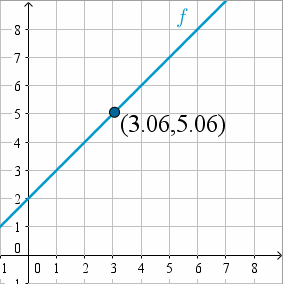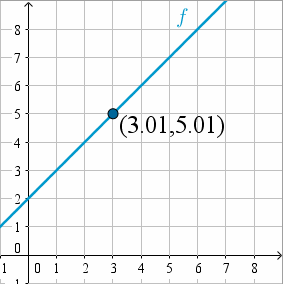
Fuente: Geogebra
Por estas razones, decimos que el límite de f en x = 3 es 5.

Tal vez te preguntes cuál es la diferencia entre el límite de f en x = 3 y el valor de f en x = 3, es decir, f(3).
Y sí, el límite de f(x) = x + 2 en x = 3 es igual a f(3), pero este no siempre es el caso. Para entender esto, consideremos la función g. Esta función es igual a f, excepto que no está definida para x = 3.
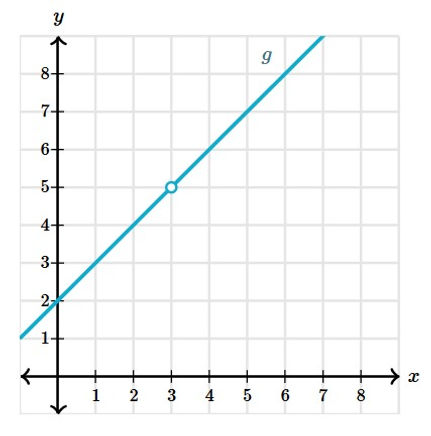
¿Qué clase de función es g?
Tal como con f, el límite de g en x = 3 es 5. Esto se debe a que aún podemos acercarnos mucho a x = 3 y los valores de la función se acercarán muchísimo a 5.

Así que el límite de g en x = 3 es igual a 5, ¡pero el valor de g en x = 3 no está definido! ¡No son lo mismo!
Esa es la belleza de los límites: no dependen del valor real de la función en el límite. Describen cómo se comporta la función al acercarse al límite.
Problema 1
Esta es la gráfica de h.